Homogeneous tree
In descriptive set theory, a tree over a product set 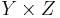 is said to be homogeneous if there is a system of measures
is said to be homogeneous if there is a system of measures 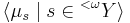 such that the following conditions hold:
such that the following conditions hold:
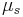 is a countably-additive measure on
is a countably-additive measure on 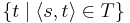 .
.- The measures are in some sense compatible under restriction of sequences: if
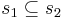 , then
, then 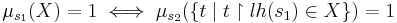 .
. - If
 is in the projection of
is in the projection of  , the ultrapower by
, the ultrapower by 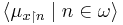 is wellfounded.
is wellfounded.
An equivalent definition is produced when the final condition is replaced with the following:
- There are
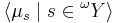 such that if
such that if  is in the projection of
is in the projection of ![[T]](/2012-wikipedia_en_all_nopic_01_2012/I/d6a1b4355a0959b0905af7a900c2dd56.png) and
and 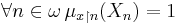 , then there is
, then there is 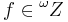 such that
such that 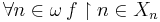 . This condition can be thought of as a sort of countable completeness condition on the system of measures.
. This condition can be thought of as a sort of countable completeness condition on the system of measures.
 is said to be
is said to be  -homogeneous if each
-homogeneous if each 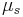 is
is  -complete.
-complete.
Homogeneous trees are involved in Martin and Steel's proof of projective determinacy.
References
- Martin, Donald A. and John R. Steel (Jan., 1989). "A Proof of Projective Determinacy". Journal of the American Mathematical Society (Journal of the American Mathematical Society, Vol. 2, No. 1) 2 (1): 71–125. doi:10.2307/1990913. JSTOR 1990913.